Radial-Polarization converter

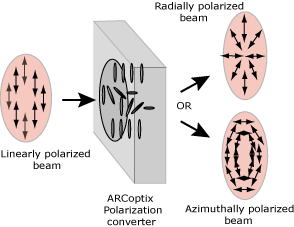
The Radial Polarization converter (RPC)from ARCoptix is a worldwide unique device that converts a conventional linearly polarized beam into a beam that has a CONTINUOUS radial or azimuthal Polarization distribution and stable in time. As illustrated in the figure below the orientation of the Polarization vector varies spatially but locally the Polarization state is considered as linear.

Thanks to the special alignment of the liquid crystal molecules, the Polarization converter rotates locally the orientation of the linearly polarized beam. Depending of the settings of the device, we may obtain either azimuthally or a radially polarization distribution at the output as described in the figure above.

The RPC can be ordered in different options (with phase compensator and TN cell) depending of your application..


Housing


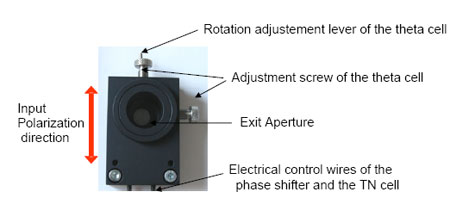
Product Overview
Generation of Laguerre-Gaussian beam (LG beam or doughnut beam)

With the help of the Arcoptix RPC, LG beams and also Bessel-Gauss beam can relatively easily be generated from any laser in the VIS-NIR region (including also pulsed lasers)

By simply focalizing (here NA 0.9) an azimuthal collimated laser beam that has passed through the Polarization converter, we obtain a typically doughnut beam as shown on the left figure here below. With the help of a linear polarizer parallel to X and Y axis, we obtain respectively the the two-half-lobes spots corresponding to x-y Polarization components of the same doughnut beam (figures in the center).

By inserting an additional annular slit in the setup, we obtain focused annular azimuthal beam (here with a NA 0.9 objective) generating so a 1st order Bessel-Gauss beam or also called vortex beams (figure on the right).


Doughnut beam (LG beam)

x-Polarization of the
doughnut beam

y-Polarization of the
doughnut beam

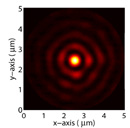
1st order Bessel-Gauss beam


Results obtained by Myun-Sik Kim at EPFL Neuchâtel with the Arcoptix RPC

For further information contact ARCoptix: info@arcoptix.com

Principle

The radial Polarization converter (RPC)is a nematic liquid crystal cell composed of one uniform and one circularly rubbed alignment layer. The local alignment of the LC in the Polarization converter is that of a twisted cell, with a twist angle given by the local alignment layers These twist angles are always smaller than pi/2. Due to (right-left rotation of the twist) a thin disinclination line appears in the LC cell (line in the figure below) but is unnoticeable for most types of experiments. As shown in figure above, when linearly polarized light is shining through a Polarization converter and the Polarization direction is parallel or perpendicular to the uniform alignment layer, azimuthally or radially polarized light emerges on the other side. So, by simple rotation of the entrance Polarization, the polaroptic Polarization converter can switch from radial to azimuthal Polarization distribution. A more detailed description can be found in "Stalder et. al., Optics Letters, volume 21, page 1948, published in 1996".


Front view LC molecule twist inside the theta-cell
Radial Polarization converter Specs
Features Radial Polarization converter
Wavelength range 350-1700 nm
Active area 10 mm diameter
Transmission better than 75% (in the VIS)
Retarder material Nematic Liquid-Crystal
Substrates material Glass bk7
Local extinction ratio (input Intensity/ouput intensity)
when placed between crossed polarizers		 ~100 @ 633nm
Output intensity homogenity < 1/100 RMS variation
Temperature range 15° - 35°
Safe operating limit 500 W/cm2 CW
300 mJ/cm2 10 ns, visible
200 mJ/cm2 10 ns, 1064 nm
Total size of the housing 6 cm x 4 cm x 1.5 cm
Applications
Doughnut focal point (or reduced size focal spot)

For some applications, such as confocal microscopy for example, one is interested to produce a doughnut shaped focal point at the front focal plane of a high NA objective. Rigorous electromagnetic calculation shows that doughnut shaped focal points can be obtained by focusing beams having a radial Polarization distribution. This may lead to interesting applications in the field of fluorescence microscopy.

Polarization axis finder (PAF)

When a Polarization converter is used in combination with a polarizer, the device results that can be used as Polarization axis finder (PAF). Watching the PAF a dark segment appears when the entrance Polarization is linear. The orientation of the dark segment gives the direction of the Polarization.

Inspection of birefringent materials: When placing a brefrigent material between two PAFs (two polarizers with two Polarization converters), one can analyze the birefringent properties of the sample in one glimpse (characteristic interference colors and main axis). Neither the sample nor the polarizers have to be rotated.

Optical trapping or optical twizers

A Doughnut shaped focal point created by focusing a radial polarized beam may increase the traping force. Also it may enable trapping particles with lower refractive index than its surrounding fluid.

Laser cutting

The Polarization direction of a laser beam when cutting materials is an important parameter. The cutting speed using p-polarized light is more than twice as fast compared to using s-polarized light. Most cutting machines are therefore releasing circular polarized light which results in an average cutting speed and in cutting direction independence. Radially polarized light may eventually increase cutting speed compared to circular polarized light... In principle the Polarization converter can withstand high intensities (500W/cm^2).

Enhanced fields in Z direction

The RPC is mostly used for creating radial polarized beams that can be focalized and obting so a strong electric field in the Z direction. This technic is used in atomic force Microscopy (AFM) and nanoparticles.

Driver (optional)

The Polarization converter can be driven with one or two standard laboratory function, generators but it can also be driven by the USB ARCoptix LC Driver.

The Arcoptix LC (Liquid Crystal) driver is a USB computer controlled electrical power supply optimized for driving the Polarization converter. The variable phase retarder (phase step compensation) and the TN cell (switch between azimuthal and radial Polarization) inside the Polarization converter can be driven with the four outputs of the LC Driver.

The LC driver has four independent outputs (Lemo connectors). They are controlled via a simple windows compatible software. The output has a variable square amplitude with polarity inversion and a frequency of 1.6 KHz. This guarantees a homogenous variation of the LC layer inside the cell. An external trigger input can be provided on demand.

References

We have already sold our radial Polarization converter all over the world. Some groups have already obtained interesting results, here are some references of articles where the LC radial Polarization converter has been used:

  1. M. Stalder and M. Schadt, "Linearly polarized light with axial symmetry generated by liquid-crystal Polarization converters," Opt. Lett. 21, p. 1948- (1996)
  2. S.F Periera and al. "Frequency spectra and waveguiding of a family of daisy modes in vertical-cavity surface-emitting lasers", opt. comm. 179, p.485, (2000).
  3. E. Descrovi and al., "Collection of transverse and longitudinal fields by means of apertureless nanoprobes with different metalic coating characteristics", appl. phys. lett. 85 (22), p. 5340, (2004). Articles may be obtained upon request.
  4. J. S. Ahn, H. W. Kihm, J. E. Kihm, D. S. Kim, and K. G. Lee, "3-dimensional local field Polarization vector mapping of a focused radially polarized beam using gold nanoparticle functionalized tips", Optics Express, Vol. 17, 14, P.2280 (2009).
  5. D. Ivanov, V. Shcheslavskiy, I. Marki, M. Leutenegger and T. Lasser, "High volume confinement in two-photon total-internal-reflection fluorescence correlation spectroscopy", appl. phys. lett. 94, 083902-1 (2009).
  6. R. Martinez-Herrero, P.M. Mejias *, G. Piquero, V. Ramirez-Sanchez, "Global parameters for characterizing the radial and azimuthal Polarization content of totally polarized beams", Optics Communications 281, p. 1976 - 1980, (2008).
  7. H. Tomizawa, H. Hanaki, T. Ishikawa,"NON-DESTRUCTIVE SINGLE-SHOT 3-D ELECTRON BUNCH MONITORWITH FEMTOSECOND-TIMING ALL-OPTICAL SYSTEM FOR PUMP & PROBE EXPERIMENTS", Proceedings of FEL 2007, Novosibirsk, Russia.
  8. F. Snik, T. Karalidi, and C. U. Keller "Spectral modulation for full linear polarimetry", Applied Optics, Vol. 48, Issue 7, pp. 1337-1346 (2009).
  9. Hong Kang, Baohua Jia, Jingliang Li, Dru Morrish, and Min Gu "Enhanced photothermal therapy assisted with gold nanorods using a radially polarized beam", APPLIED PHYSICS LETTERS 96, 063702 (2010).
  10. Eyal Shafran, Benjamin D. Mangum, and Jordan M. Gerton, "Energy Transfer from an Individual Quantum Dot to a Carbon Nanotube", Nano Letters 2010 10 (10), 4049-405
  11. V. Ramirez-Sanchez, G Piquero and M Santarsiero "Generation and characterization of spirally polarized fields", J. Opt. A: Pure Appl. Opt. 11 (2009) 085708 (6pp).
  12. Zachary D. Schultz, Stephan J. Stranick and Ira W. Levin, "Advantages and Artifacts of Higher Order Modes in Nanoparticle-Enhanced Backscattering Raman Imaging", Anal. Chem., 2009, 81 (23), pp 9657 - 9663
  13. I. Rajapaksa, K. Uenal, and H. Kumar Wickramasinghe " Image force microscopy of molecular resonance: A microscope principle", APPLIED PHYSICS LETTERS 97, 073121 (2010).
  14. Jeffrey A. Davis and co-Authors, "Vortex sensing analysis of radially and pseudo-radially polarized beams", Optical Engineering, Vol(52)5, May 2013.
  15. Du Fu-Rong and co-Authors, "Experimental verification on tightly focused radially polarized vortex beams", Chin. Phys. B Vol. 22, No. 6 (2013).
  16. Min Gu, Han Lin, and Xiangping Li,"Parallel multiphoton microscopy with cylindrically-polarized multifocal arrays", Optics letters, 2013.
  17. Hyun Woo Kihm and co-AUthors, "Optical magnetic field mapping using a subwavelength aperture", Optics Express, Vol. 21, Issue 5, pp. 5625-5633 (2013).
  18. Yikai Chen and Co-Authors, "Surface-plasmon-coupled emission microscopy with a Polarization converter", Optics Letters, Vol. 38, Issue 5, pp. 736-738 (2013).
  19. Hao Wang and Zachary D. Schultz, "The chemical origin of enhanced signals from tip-enhanced Raman detection of functionalized nanoparticles", Analyst , 2013, 138, 3150 - 3157.
  20. A C Assafrao and Co-Authors, "Experimental and theoreticalinvestigation on the misalignment tolerance of a micron-sized solid immersion lens", J. Opt. 15 (2013) 025706 (6pp).
  21. Yuen Yung Hui, "Tip-enhanced sub-diffraction fluorescence imaging of nitrogen-vacancy centers in nanodiamonds", Appl. Phys. Lett. 102, 013102 (2013).
  22. Lin, Jian et al. Radially polarized tip-enhanced near-field coherent anti-Stokes Raman scattering microscopy for vibrational nano-imaging, Appl, phys Letter, Vol 103 (8) (2013).
  23. Lin, Jian et al. Radially polarized tip-enhanced near-field coherent anti-Stokes Raman scattering microscopy for vibrational nano-imaging, Appl, phys Letter, Vol 103 (8) (2013).
  24. Xiangping Li, Tzu-Hsiang Lan, Chung-Hao Tien2 & Min Gu ,"Three-dimensional orientation-unlimited Polarization encryption by a single optically configured vectorial beam", Nature Communications 3 (2013).
  25. Deepa, S., B.S., B.R. & Senthilkumaran, P. Helicity dependent diffraction by angular momentum transfer. Sci Rep, 9, 12491 (2019).
  26. Rocio Camacho-Morales & al., Resonant harmonic generation in AlGaAs nanoantennas probed by cylindrical vector beams,Nanoscale, 28 January 2019, Issue 4.
  27. Fajun Xiao & al.,Selective excitation of a three-dimensionallyoriented single plasmonic dipole, Photonics Research, Vol. 7, No. 6, June 2019.
  28. Optical trapping of nanoparticles by full solid-angle focusing
  29. Godofredo Bautista, Christoph Dreser, Xiaorun Zang, Dieter P. Kern, Martti Kauranen, and Monika Fleischer, Collective Effects in Second-Harmonic Generation from Plasmonic Oligomers, Nano Letters 2018,18, (4),2571-2580
  30. Krasavin, A.V., Segovia, P., Dubrovka, R. et al. Generalization of the optical theorem: experimental proof for radially polarized beams. Light Sci Appl 7, 36 (2018)
  31. Haidan Mao & al., Self-steering partially coherent vector beams, OPTICS Express, Vol. 27, No. 10, 13 May 2019.
  32. and many mores...